本文共 2990 字,大约阅读时间需要 9 分钟。
1. 基本概念
1.1 MXNet相关概念
深度学习目标:如何方便的表述神经网络,以及如何快速训练得到模型
CNN(卷积层):表达空间相关性(学表示)
RNN/LSTM:表达时间连续性(建模时序信号) 命令式编程(imperative programming):嵌入的较浅,其中每个语句都按原来的意思执行,如numpy和Torch就是属于这种
声明式语言(declarative programing):嵌入的很深,提供一整套针对具体应用的迷你语言。即用户只需要声明要做什么,而具体执行则由系统完成。这类系统包括Caffe,Theano和TensorFlow。命令式编程显然更容易懂一些,更直观一些,但是声明式的更利于做优化,以及更利于做自动求导,所以都保留。
| 浅嵌入,命令式编程 | 深嵌入,声明式编程 | |
| 如何执行a=b+1 | 需要b已经被赋值。立即执行加法,将结果保存在a中。 | 返回对应的计算图(computation graph),我们可以之后对b进行赋值,然后再执行加法运算 |
| 优点 | 语义上容易理解,灵活,可以精确控制行为。通常可以无缝的和主语言交互,方便的利用主语言的各类算法,工具包,bug和性能调试器。 | 在真正开始计算的时候已经拿到了整个计算图,所以我们可以做一系列优化来提升性能。实现辅助函数也容易,例如对任何计算图都提供forward和backward函数,对计算图进行可视化,将图保存到硬盘和从硬盘读取。 |
| 缺点 | 实现统一的辅助函数和提供整体优化都很困难。 | 很多主语言的特性都用不上。某些在主语言中实现简单,但在这里却经常麻烦,例如if-else语句 。debug也不容易,例如监视一个复杂的计算图中的某个节点的中间结果并不简单。 |
1.2 深度学习的关键特点
(1)层级抽象
(2)端到端学习
2. 比较表
| 比较项 | Caffe | Torch | Theano | TensorFlow | MXNet |
| 主语言 | C++/cuda | C++/Lua/cuda | Python/c++/cuda | C++/cuda | C++/cuda |
| 从语言 | Python/Matlab | - | - | Python | Python/R/Julia/Go |
| 硬件 | CPU/GPU | CPU/GPU/FPGA | CPU/GPU | CPU/GPU/Mobile | CPU/GPU/Mobile |
| 分布式 | N | N | N | Y(未开源) | Y |
| 速度 | 快 | 快 | 中等 | 中等 | 快 |
| 灵活性 | 一般 | 好 | 好 | 好 | 好 |
| 文档 | 全面 | 全面 | 中等 | 中等 | 全面 |
| 适合模型 | CNN | CNN/RNN | CNN/RNN | CNN/RNN | CNN/RNN? |
| 操作系统 | 所有系统 | Linux, OSX | 所有系统 | Linux, OSX | 所有系统 |
| 命令式 | N | Y | N | N | Y |
| 声明式 | Y | N | Y | Y | Y |
| 接口 | protobuf | Lua | Python | C++/Python | Python/R/Julia/Go |
| 网络结构 | 分层方法 | 分层方法 | 符号张量图 | 符号张量图 | ? |
3.详细描述
3.1 MXNet
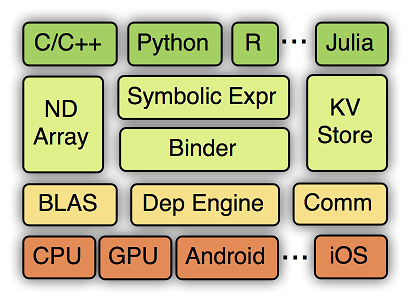
MXNet的系统架构如下图所示:
从上到下分别为各种主语言的嵌入,编程接口(矩阵运算,符号表达式,分布式通讯),两种编程模式的统一系统实现,以及各硬件的支持。
MXNet的设计细节包括:符号执行和自动求导;运行依赖引擎;内存节省。
3.2 Caffe
优点:
1)第一个主流的工业级深度学习工具。 2)它开始于2013年底,由UC Berkely的Yangqing Jia老师编写和维护的具有出色的卷积神经网络实现。在计算机视觉领域Caffe依然是最流行的工具包。
3)专精于图像处理
缺点:
1)它有很多扩展,但是由于一些遗留的架构问题,不够灵活且对递归网络和语言建模的支持很差。
2)基于层的网络结构,其扩展性不好,对于新增加的层,需要自己实现(forward, backward and gradient update)
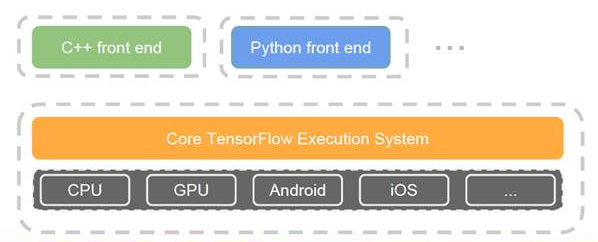
3.3 TensorFlow
优点:
1) Google开源的其第二代深度学习技术——被使用在Google搜索、图像识别以及邮箱的深度学习框架。
2)是一个理想的RNN(递归神经网络)API和实现,TensorFlow使用了向量运算的符号图方法,使得新网络的指定变得相当容易,支持快速开发。
3)TF支持使用ARM/NEON指令实现model decoding
4)TensorBoard是一个非常好用的网络结构可视化工具,对于分析训练网络非常有用
5)编译过程比Theano快,它简单地把符号张量操作映射到已经编译好的函数调用
缺点:
1) 缺点是速度慢,内存占用较大。(比如相对于Torch)
2)支持的层没有Torch和Theano丰富,特别是没有时间序列的卷积,且卷积也不支持动态输入尺寸,这些功能在NLP中非常有用。
3.4 Torch
优点:
1)Facebook力推的深度学习框架,主要开发语言是C和Lua
2)有较好的灵活性和速度 3)它实现并且优化了基本的计算单元,使用者可以很简单地在此基础上实现自己的算法,不用浪费精力在计算优化上面。核心的计算单元使用C或者cuda做了很好的优化。在此基础之上,使用lua构建了常见的模型
4)速度最快,见
5)支持全面的卷积操作:
- 时间卷积:输入长度可变,而TF和Theano都不支持,对NLP非常有用;
- 3D卷积:Theano支持,TF不支持,对视频识别很有用 缺点
1)是接口为lua语言,需要一点时间来学习。
2)没有Python接口
3)与Caffe一样,基于层的网络结构,其扩展性不好,对于新增加的层,需要自己实现(forward, backward and gradient update)
4)RNN没有官方支持
3.5 Theano
优点:
1)2008年诞生于蒙特利尔理工学院,主要开发语言是Python
2)Theano派生出了大量深度学习Python软件包,最著名的包括Blocks和Keras
3)Theano的最大特点是非常的灵活,适合做学术研究的实验,且对递归网络和语言建模有较好的支持
4)是第一个使用符号张量图描述模型的架构
5)支持更多的平台
6)在其上有可用的高级工具:Blocks, Keras等
缺点:
1)编译过程慢,但同样采用符号张量图的TF无此问题
2)import theano也很慢,它导入时有很多事要做
3)作为开发者,很难进行改进,因为code base是Python,而C/CUDA代码被打包在Python字符串中
参考资料:
1)
2)
3)